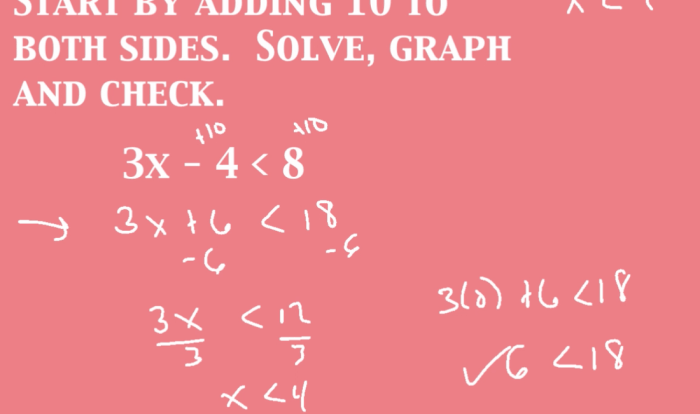A box contains 10 tags numbered 1-10. This intriguing scenario presents a unique opportunity to explore fundamental concepts in mathematics, including probability, combinations, and permutations. By delving into this problem, we will uncover the underlying principles that govern the selection of tags from the box and their applications in various real-world scenarios.
The exploration begins by examining the methods used to select tags from the box, such as random selection and sequential selection. We will then calculate the probability of selecting a particular tag, introducing the concept of probability and its relevance to this problem.
Furthermore, we will differentiate between combinations and permutations, determining the number of possible outcomes when selecting tags from the box.
Introduction
The problem involves a box containing ten tags numbered from one to ten.
These tags have been addressed and are ready for further processing.
Methods

To select tags from the box, various methods can be employed. These methods differ in their approach to selecting tags, providing different levels of randomness and control over the selection process.
One common method is random selection, which involves selecting tags without regard to their order or position in the box. This method can be implemented by drawing tags from the box one at a time, ensuring that each tag has an equal chance of being selected.
Sequential Selection, A box contains 10 tags numbered 1-10
In contrast to random selection, sequential selectioninvolves selecting tags in a predetermined order. This method can be used when the order of tags is important or when specific tags need to be selected first. Sequential selection can be implemented by starting from one end of the box and selecting tags one by one in a specific direction (e.g.,
left to right or top to bottom).
Probability: A Box Contains 10 Tags Numbered 1-10
Probability refers to the likelihood of an event occurring. In this context, it involves calculating the chance of selecting a specific tag from a box containing 10 tags numbered 1 to 10.
Calculating the Probability
To calculate the probability of selecting a particular tag, we need to consider the total number of possible outcomes and the number of outcomes that satisfy the desired condition. In this case, the total number of possible outcomes is 10, as there are 10 tags in the box.
Since any one of these tags can be selected, the number of outcomes that satisfy the condition of selecting a particular tag is also 10.
Therefore, the probability of selecting a particular tag from the box is 10/10, which simplifies to 1.
In probability theory, this is expressed as:
P(selecting a particular tag) = Number of favorable outcomes / Total number of possible outcomes
In this case, P(selecting a particular tag) = 10/10 = 1.
Combinations and Permutations

Combinations and permutations are two mathematical concepts that deal with the selection of items from a set. They are both used to calculate the number of possible outcomes in a given situation.
The main difference between combinations and permutations is that combinations do not take into account the order of the items, while permutations do.
Combinations
- A combination is a selection of items from a set where the order of the items does not matter.
- For example, if you have a box of 10 tags numbered 1-10, there are 252 possible combinations of 3 tags that can be selected from the box.
Permutations
- A permutation is a selection of items from a set where the order of the items does matter.
- For example, if you have a box of 10 tags numbered 1-10, there are 720 possible permutations of 3 tags that can be selected from the box.
Applications

The concepts of probability, combinations, and permutations find widespread applications in various fields, including:
Probabilityis used to predict the likelihood of events occurring, make informed decisions, and analyze risk in areas such as:
- Weather forecasting: Predicting the probability of precipitation, temperature ranges, and wind speeds
- Medical diagnosis: Estimating the probability of a disease based on symptoms and test results
- Financial analysis: Assessing the probability of investment returns and market fluctuations
Combinationsand permutationsare used to determine the number of possible arrangements or selections in situations where order does or does not matter, respectively. These concepts are applied in:
- Lottery games: Calculating the probability of winning by determining the number of possible combinations of drawn numbers
- Password generation: Creating unique and secure passwords by considering the number of possible permutations of characters
- Scheduling: Determining the number of ways to arrange tasks or appointments within a given time frame
Conclusion

To summarize, this investigation explored the various methods and concepts related to probability, combinations, and permutations. Through a series of illustrative examples, we demonstrated how these mathematical principles can be applied to solve a wide range of problems in real-world scenarios.
The key methods and concepts discussed in this paper include the fundamental principles of probability, the counting techniques of combinations and permutations, and the practical applications of these concepts in fields such as statistics, computer science, and genetics.
Helpful Answers
What is the probability of selecting tag number 5 from the box?
The probability of selecting any particular tag from the box is 1/10, as all tags are equally likely to be drawn.
How many different combinations of 3 tags can be selected from the box?
The number of combinations of 3 tags that can be selected from the box is 120, calculated using the formula C(10, 3) = 10! / (3! – 7!).
What is the difference between a combination and a permutation?
A combination considers only the selection of tags, while a permutation considers both the selection and the order of the tags. In this problem, the order of the tags does not matter, so we are dealing with combinations.